‘To See a World in a Grain of Sand’: A Deep-Dive Into the Universe of Fractal Infinities
In this dynamic world, nothing remains still, everything flows. Even so, these microcosmic shapes are able to capture a natural order going on behind-the-scenes.
Online fractal-generating software such as JWildfire are able to create aesthetic images from a diverse selection of basic patterns. This breathtaking fractal shows self-similarity through the white ring in the foreground and the tiny quartets which echo this shape deep into the background.
Nature reveals itself in a daze. The branches of trees split in a frenzy, ocean waves crash over the shores. Above us, the ashes of stars muster to form new constellations. Below us, bacterial colonies shuffle in lush microbial jungles. Within our own lives, we are given to spells of spontaneity as we drift along the stream of present moments. It is all in flux, as the chaos of forces entangles our universe.
But while entropy tells us the universe is fated to disorder in the long run, there exists a bizarre sense of order underlying its complex dynamics. These peculiar patterns of nature crop up around every corner. They are small, yet larger than life; they are timeless, yet freshly new. They are kaleidoscopic peepholes through which we can gaze at the universe’s inner workings. Enter, the fractal.
What is a Fractal?
Fractals are a seeming paradox: extraordinary yet hidden in plain sight, these patterned shapes exhibit an endless degree of complexity. You might know them as the shapes that have a finite area but infinite perimeter. Fractals reveal this through a special property called self-similarity, meaning that zooming in on any part of the fractal can leave you looking at a replica of the whole. Self-similarity gives fractals this quality of appearing fragmented and irregular, but in another sense, they are uniquely geometric.
Interestingly, the intricacies of fractals can be captured by repeating simple algorithms in a process known as recursion, where the results of one generation are the culmination of previous generations. Take a look at a tree. First, you see the wide reach of the trunk. Then you see large branches growing out of the stem. Out of these large branches, smaller limbs pop up, and out of them, even tinier twigs appear, and so on. With each magnification into the tree, finer and finer branches emerge for up to eleven orders of branches. Many dynamic forces of nature grant this level of attention to detail, from the flow of water down a stream to the crack of lightning. As such, fractals are the animated picture of chaos emerging from simplicity, able to seamlessly describe many of the fluid phenomena around us and across the universe.
Fractal patterns can be created with pencil and paper. For example, if you repeatedly divide a triangle into smaller and smaller portions of itself, you end up with the thinly serrated Sierpiński Triangle. Or, by continuously drawing smaller and smaller triangles extended out from a base triangle, you get a shape which strikingly resembles a snowflake, commonly known as the Koch Snowflake.
As a result of self-similarity, reality is quite literally bent out of shape as the ordinary conventions of length, width, and height in our 3-dimensional world no longer hold around fractals. Scaling a fractal in size is not proportional to its area or volume in the same way that scaling a 2D square or a 3D sphere augments space. Rather, many fractals occupy special non-integer Hausdorff dimensions. This means that fractals can exist on a dimension of their own, somewhere in the crevices between the 1st, 2nd, and 3rd (or possibly even higher) dimensions we are familiar with.
The Sierpiński Triangle shown earlier? A fractal dimension of about 1.585. And the Koch Snowflake? Around 1.26. To show you what these numbers mean, imagine sliding a finger along the edge of one of these objects — as a rule of thumb, the higher the dimension, the more rough and complex an object tends to be. Just about any complex shape can have a Hausdorff dimension assigned to it; in fact, the coastline of Great Britain has a Hausdorff dimension of approximately 1.21!
This all might boggle with your notion of what a ‘dimension’ is, but as it is understood, fractional dimensions refer to how well an object fills up its surrounding space. Think of a piece of paper, which is practically 2D. In contrast, a 3D pile of paper will fill up more space because it occupies another dimension of depth. But when you crumple that piece of paper, you now have a shape that fills up more space than the flat sheet of paper, but less than the pile. The result is somewhere in-between — approximately 2.5-dimensional. There exists a whole continuum of these fractional dimensions in the objects around us. Fractal dimensions are further discussed in mathematician Grant Sanderson’s YouTube channel ‘3Blue1Brown.’
Discovering Fractals
Various cultures around the world have long been captivated with the fractal nature of reality. Fractals have imbued mandalas with spiritual significance in Buddhism and expressed heavenly elegance in Gothic architecture. They’ve shown up from the intricate tessellations adorning Islamic mosques to the symmetrical designs of Persian carpets woven by nomadic tribesmen. Needless to say, the arts and culture reflect our longstanding desire to mimic the aesthetics of the natural world.
But it wasn’t until the latter part of the 20th century that the fractal structures underlying these motifs would be understood. In the late ‘70s, Polish mathematician and jack-of-all-trades Benoît B. Mandelbrot sought to find a way to capture the subtleties of reality that had puzzled earlier mathematicians. As Mandelbrot believed, the rigid lines of algebra and the smooth curves of calculus were too idealized to do so. Instead, reality is in a feverish craze, “Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line,” Mandelbrot famously wrote.
Even then, Mandelbrot kept finding “order in that roughness,” as he said in a TED-Talk. That’s the big paradox — how can simplicity exist among complexity? “It’s very complicated and it’s very simple, both at the same time,” Mandelbrot elaborated. Here, Mandelbrot refers to the limited self-similarity of most natural fractals. The infinite degree of self-similarity you find in abstract shapes such as the Sierpiński Triangle or the Koch Snowflake are undeniably novel and satisfying, but they are only a subset of all the fractal shapes out there. Rather, most natural fractals are a diverse blend of the simple and the complex, somewhere in the collisions of two distinct worlds edging back and forth. Nature might show self-similarity down to microscopic, but nonetheless, non-infinitesimal scales.
Fractals were first visualized using mathematical models by putting inputs from an equation through a recursive feedback loop. This process is cycled millions of times to get a full picture of what an equation looks like, usually to moot results. But in 1980, Mandelbrot was simulating one such equation on an old-fashioned supercomputer at IBM. The equation was relatively simple (z → z² + c), yet the results were boundless in spectacle — the image went on and on and on.
Above are outstanding images from the illustrious Mandelbrot set named after him. Notice that the same bulb-like formation is a running theme throughout the set, and as you go further down, each bulb is accompanied by more complex detail than the last. As it turned out, the precision of these details was limited only to the power of the machine computing the equation, as self-similar shapes would continue on forever at an infinite scale. Mandelbrot’s breakthrough had uncovered a new form of geometry, there were rules to this roughness, but it was one which had never before been identified by the scientific community. In 1975, Mandelbrot coined the term ‘fractal’ after the Latin word fractus for ‘fragmented’ or ‘broken’ for this exquisite shape.
Since then, the Mandelbrot set has been frequently dubbed the ‘poster child of mathematics’ and has served as the icon for the burgeoning field of chaos theory, which seeks to understand the mechanics behind the natural disorder present everywhere in the universe. More recently, numerous online videos have surfaced which zoom into the Mandelbrot set down to subatomic scales.
Mandelbrot will always be renowned for his discovery of fractal geometry, but he should also be revered for bridging the gap between the arts and mathematics, and demonstrating that these two worlds are not mutually exclusive, but are enmeshed under the natural elements. His insights teach us that visualization and an inclination to change perspectives may be the unexpected key to solving the world’s most difficult problems, by challenging our preconceptions and revealing connections previously unseeable to the naked eye.
Flora, Fractal, Fauna
Fractals are so compelling because they abundantly make up the backbone of nature. They are a strange byproduct of the universe’s physical laws coming into fruition. In many cases, this is because fractal patterns encapsulate the most effective way to streamline energy throughout an ecosystem.
Biological life has its fair share of fractal structures. Take a look at the leaves of a fern plant: each leaf is a miniature version of the whole. Or the Romanesco Broccoli, one of the most novel fractals, whose large buds contain an intimate landscape of tiny buds, and these tiny buds contain even tinier buds of their own, and so on. The florets of some flowers, such as the sunflower, are arranged along Fermat’s spiral (a special angle with the properties of the golden ratio) to create a photogenic, spiraling flowerhead. Spiral structures are especially common, such as those found atop hurricane storms or those entwining seashells.
Fractals are even a component of our anatomy. We humans are born with intricately-woven blood vessels tracking the whole volume of our body. Altogether, our blood vessels stretch an impressive 60,000 miles in length, but by forming in a fractal pattern, our bodies ensure that every nook-and-cranny is covered to maintain the optimal bodily temperature. The same is true for the distribution of bronchioles in our lungs, which expand in every direction like the roots of a tree to maximize gas exchange with oxygen.
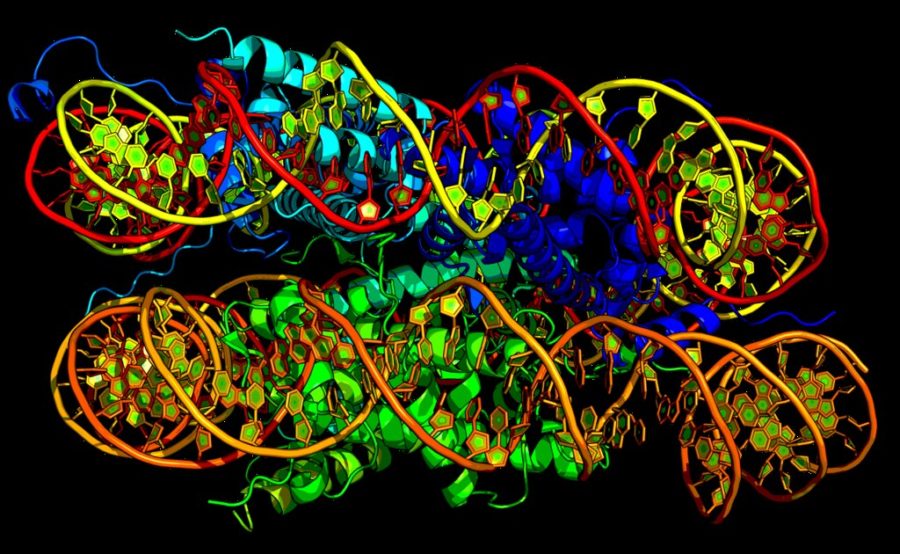
Additionally, scientists have long known that DNA is arranged in a double helix. But if it did not fold any further, each cell’s genome could extend to two meters long, far too large for the nucleus of any human cell to contain. In 2009, scientists at MIT, Harvard, and UMass Medical School revealed the ingenious 3-dimensional folding of the human genome that allows each cell to remember some three billion base pairs of DNA without overlap.
Their data indicates that the genome is organized into two separate compartments, keeping active genes accessible while cloistering unused DNA in a denser compartment. After collaborating with physicists at MIT, genome scientists established that the result of this arrangement is a fractal structure known as a ‘fractal globule’ which enables it to pack DNA incredibly tightly while simultaneously avoiding any knots that might hinder gene functioning. This has several advantages to other models, enabling DNA to easily unfold and refold during gene expression, gene repression, and cell replication. This discovery provides a new dimension to study the genome in the future. In essence, the idea is that the best way to fill a space is to form a fractal structure.
It is no mistake that such fractals appear plentifully in Earth’s biology. Natural selection drives living creatures to adapt to the world around them. Oftentimes, this involves remaining as simple as possible while still being able to survive. Nature presents an elegant solution to this conundrum. It is often easier, physically and biologically, to follow self-similar fractal patterns than to expend unnecessary energy on specific structures. ‘Form follows function’ is the principle here. If it weren’t for fractals, it is plausible that organic life would never have been able to emerge from the primordial soup eons ago in Earth’s history.
Non-biological processes demonstrate fractal features too. The microscopic structure of snowflakes shows symmetry along six sides, recalling the famous saying ‘No two snowflakes are alike.’ The flow of water, wind, and other sources of erosion form fractal patterns over coastlines, sand dunes, and mountains. These structures are meticulously molded into shape through the ages. Analogous to friction or air resistance, the topology of Earth’s landscape is dampened, forming a colossal fractal structure the size of landscapes.
Fractals occur over Earth’s terrain for similar reasons as they do in its biology. The constant wear-and-tear acting on objects gives rise to recursion. This intensifies the lay of the land, skewing it, and results in self-similar crags, divots, and ridges. The persistent action of a waterfall can introduce cracks to a rock bed underneath, thereby prompting a fractal. On the geological scale, this means that successive strata topple the layers of bedrock from past eras. Over a lifetime, it can be puzzling to notice the impermanent pictures around us; the changing face of the planet is sculpted over vast stretches of time.
Fractals are flexible objects that pop up everywhere in nature. It’s emboldening to know that nature embodies these shapes without any direct impetus to do so. No laws of the universe govern that the fractal should manifest where they do, no single process produces fractals as if they were chemical reactions. “Finding fractals is kind of like uncovering dinosaur fossils from millions of years ago. Or, like putting a soup of the natural elements to a stir. It’s a matter of pattern recognition, really,” says Nahiyan Islam ‘24.
The Connected World
Understanding fractals ushers in a cornucopia of insights into the world around us. Fractals have advanced various fields of science: including biology, cosmology, neurology, programming, physics, technology, and countless more. It might be that the fractal nature of many phenomena reveals just how interconnected the universe really is.
For instance, our brains have a peculiar relationship with fractal structures. The human brain is one of the most complex structures out there — it consists of over 80 billion neurons, the cells that process the senses and send signals throughout the body. In a space the size of 10 tennis balls, neurons are intricately networked via axons and dendrites to make the over 100 trillion connections we need to go about our lives. In doing so, the neuron branching exhibits a considerable fractal dimension of about 2.80 for a scale of up to 3 millimeters.
In 2003, biophysicist John M. Beggs and Chief of the Section on Critical Brain Dynamics Dietmar Plenz at the National Institute of Mental Health in Maryland discovered that networks of neurons perform best under complex dynamics predicted by self-similarity during information transmission. This property occurs in the phase transition between two states, the edges of order and disorder over what is known as the critical point. Sounds familiar? It may be that fractal patterns are advantageous to our perception.
According to the critical brain hypothesis, the brain hovers over the critical point in its equilibrium state to optimize neuron transmission at all scales. When the environment is prone to rupture, remaining sensitive to spurts of neuronal activity can mean leveraging vitality when it matters. Neurons do this by sending out information avalanches to other neurons in the vicinity, which initiates a self-similar cascade of events over the network. In this way, slight changes could result in big, complex behaviors across the brain. Ongoing research into critical theory attempts to locate more fractals in the brain’s wiring to enhance this model. If not for fractal dynamics, it is plausible that the human consciousness that makes up who you are would not be able to operate.
Now, let’s zoom out to larger scales. Let’s say you point a space telescope at a remote patch of space, where the glistening planets, comets, and stars speckle the darkness. Puzzlingly enough, at great scales, the composition of the deep cosmos might bear a striking resemblance to the neuron branching of the brain. Perceiving a connection between these phenomena despite their vast disparities in size might seem like far-fetched pareidolia (our tendency to grasp meaning in the ambiguous visual patterns around us) — but take a look through the images below; I daresay something is going on here.
Outer space, like the neurons in your brain, is a highly networked structure. The universe we can observe with our current scientific equipment is referred to as the observable universe, which spans 93 billion light-years across and contains stars currently on the order of the sextillions (10²³, a ‘1’ followed by 23 zeros). These galaxies, including our Milky Way, each contain billions of stars and are grouped into clusters of galaxies. Our Milky Way is part of the Local Group, a body of around 80 galaxies in the celestial neighborhood.
But it just keeps going. Our Local Group is itself part of a wider region of galaxies known as the Virgo Supercluster, containing about 2,000 galaxies, which is then embedded in the gigantic Laniakea Supercluster, home to an astronomical 100,000 galaxies sweeping out 520 million light years of space. Zooming out of the universe in this way reveals a wide distribution of self-similarity for up to around 107 megaparsecs, or 350 million light years across, before everything becomes roughly homogenized, the WiggleZ Dark Energy Survey finds.
While the internal universe may not be one gigantic fractal, the tremendous stretches of space between its galactic groups and clusters are not voids; rather, they are packed with connecting tendrils of both ordinary and dark matter (an invisible type of matter thought to be responsible for gravitational anomalies) that stretch for millions of light years, known as filaments.
On a macroscopic scale, the big picture assembled by these filaments is a foam-like structure known as the Cosmic Web — which does display some fractal properties. Clumps of dark matter called halos can gravitationally anchor galaxies and superclusters in place despite the cosmic expansion of the universe, and within these halos, nested structures can form with their own sub-haloes and sub-sub-haloes inside those. You can watch mesmerizing videos of how dark matter halos evolve in the Illustris Project’s simulation and the Aquarius simulation.
Yet, put an image of the Cosmic Web and the neurons in the brain side-by-side, and something unusual happens — they look one and the same. Spatially, the two could not be farther apart, so what is happening here? What could the structure of the universe have anything to do with the structure of the brain? Such questions were asked by Franco Vazza, an astrophysicist at the University of Bologna, and Alberto Feletti, a neurosurgeon at the University of Verona, who collaborated to quantify the visual similarities in these phenomena.
After extensive analysis, their findings indicate that the Cosmic Web and neurons display a “remarkable” similarity over certain scales where both structures are still fractal (0.01-1.6mm for the brain, and 1-100 megaparsecs for the cosmos). Scale is crucial here, as neither the neurons of the brain nor the filaments of the Cosmic Web are entirely self-similar. This property suggests that both networks have a similar affinity for scale in spurring their creation.
This couples with other fascinating similarities between the Cosmic Web and the brain. The brain is 75% water whereas the Cosmic Web is 73% dark energy — might these materials/energies have influenced their structures? As passive material, these two are not readily a part of the structure of the brain or the Cosmic Web, but they may be relevant to how these networks form. There is something to think about.
A second intriguing similarity is that the amount of computer data required to map out the Cosmic Web is comparable to the theoretical memory storage capabilities of the human brain. 1-10 petabytes (1 petabyte = 1000 terabytes) of data is needed to map out the evolution of the universe at scales where the Cosmic Web becomes apparent. Meanwhile, estimates on the total storage capacity of the brain settle at around a staggering 2.5 petabytes. If these approximations are leading us in the right direction, it could mean that the Cosmic Web can hypothetically be stored in the brain, or the other way around, the Cosmic Web can hold the data of a lifetime of human experiences. Perhaps, in the coming future, this is better left for AI.
The study concludes by hinting that similar networking patterns can emerge from entirely different processes of nature. It may be that the broad parallel struck between the Cosmic Web and the neuron does not exist as an isolated finding, and that there exists an infinity of such connections constellating the breadth of the universe. We are on the cusps of understanding that a whole universe of connections is in our minds, a universe within a universe, one capable of realizing itself and reaching out to the much wider sphere it inhabits.
Perhaps, Vazza and Feletti’s investigation speaks true to the hopes and aspirations of science at large. The range of fractals above and below us illustrates their centrality as geometries of the universe. The next step for scientists and theoreticians, therefore, is to delve into that universe of fractal infinities.
Working With Infinity
This is the realm of theories and novel ideas, which in recent decades has become the next frontier for the latest breakthroughs in the physical sciences. You see, scientific extraordinaires have long been mystified by the notion of a ‘theory of everything’ that is conjectured to unify all aspects of the universe. Our current understanding of the universe hovers in a state of limbo as scientists have yet to construct a fundamental model encompassing both classical and modern physics.
Even so, for many physicists, the holy grail of a theory of everything stokes the flame for dedicated speculation and fierce debate into the uncharted regions of our knowledge. The feeling of discovering something momentous right around the corner resides fervently in such theorists. And their work contains a running theme — a propensity to involve fractal infinities within the workplace.
Carl Sagan, the renowned professor of astronomy at Cornell University, had anticipated this sentiment in an epiphany from his popular science book Cosmos, “There is, we are told, an infinite hierarchy of universes, so that an elementary particle, such as an electron, in our universe would, if penetrated, reveal itself to be an entire closed universe. Within it, organized into the local equivalent of galaxies and smaller structures, are an immense number of other, much tinier elementary particles, which are themselves universes at the next level, and so on forever — an infinite downward regression, universes within universes, endlessly. And upward as well.” Sagan’s extravagant vision of an infinite fractal cosmos evokes a question which has stirred at the back of the minds of some physicists for years: whether the universe exists not as a lone entity, but in the midst of infinitely many universes making up the multiverse.
While this concept is perfect for roundabout plots in comics and shows, the multiverse actually has a long-running history with the work of theoretical physicists. In 1969, Leonhard Susskind, a particle physicist at Yeshiva University, changed physics forever when he imagined the atomic world not as a jumble of spherical blobs under a medium, but as individual loops of strings which combine and vibrate to form interactions. Susskind knew it not then, but he had stumbled upon the strange world of string theory, one of the most enduring and most contentious contenders for a theory of everything. This theory has garnered many caveats and variations over the years (owing to its befuddling nature), but in general, string theory replaces the subatomic particles consisting of quarks, bosons, and leptons (the building blocks of electrons, protons, and neutrons) with one-dimensional strings of energy that wriggle in at least 10 dimensions or more to generate the building blocks of reality.
On the downside, string theory can be demanding for potential proponents given the lack of any proper gauge of the world past the 4th-dimension. Moreover, the extra six dimensions could have different shapes, sizes, and topologies that can be rearranged in a multitude of ways. Because the geometry of these dimensions is instrumental to how strings are tuned to create the particles and forces they embody, string theory allows for a mishmash of physical laws and constants. In other words, string theory reveals that the same theoretical spacetime fabric that brings elements of gravity, quantum mechanics, and the subatomic particles together also reveals that the same outcome could propagate in countless other fabrics.
For keen theorists, this meant that string theory had the potential to describe an unimaginable number of universes, 10⁵⁰⁰ in total, with each mathematical possibility realized in its own physical reality, our own universe representing but one gleaming marble in the exotic pile of the whole multiverse. This idea is called the String Theory Landscape, and though it dashes Einstein’s idea of one unified existence, it is our latest blueprint for why the universe has the properties it does.
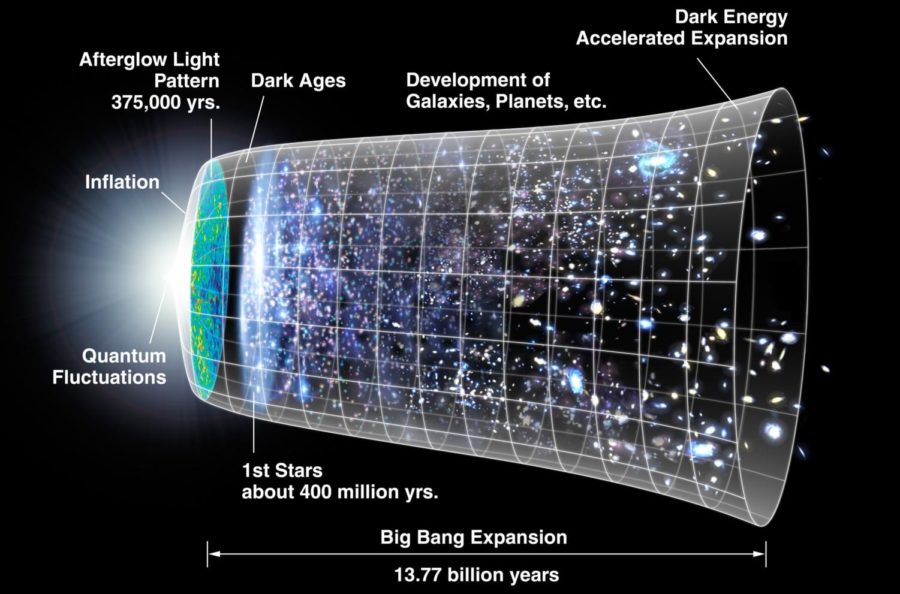
But such quantum quandaries could still be proven inadequate to describe the real world. Instead, physicists at Stanford University rewinded time to the origins of the universe with the Big Bang, seen now from the lens of newer elements offered by string theory — and another theory, cosmic inflation. Cosmic inflation holds that the Big Bang actually began with an inflationary state that shot up our universe at faster-than-speeds from a quantum fleck to a huge expanse of emptiness a quarter-billion light years wide in a shred of a second (10⁻³⁵ seconds). According to Andrei Linde, a main pioneer of cosmic inflation and a professor of physics at Stanford University, the universe rapidly leveled off from such stellar expansion like a ball rolling down a hill.
It was from this great explosion of matter that the galaxies of our universe grew out of faint quantum fluctuations in the makeup of spacetime. The concentration of matter in these regions was slightly greater compared to surrounding areas and this difference was amplified during inflation, allowing them to corral even more matter. And so, as the theory goes, the early universe had sown the seeds for the cosmos we live in today. From 1989 to 1993, NASA’s Cosmic Background Explorer (COBE) satellite observed the ancient vestiges of cosmic inflation in the form of hot and cold regions in the Cosmic Background Radiation left behind by the first rays of light that escaped the Big Bang. This undoubtedly established cosmic inflation among the standard model of cosmology.
But soon after, Linde and other physicists realized that the same quantum fluctuations that produced outer space with the Big Bang can generate new expanding regions elsewhere in the universe. While inflation stopped in our observable universe some 13.8 billion years ago, it can keep going at the outermost edges of the universe. In response to these discoveries, Linde proposed an inflationary universe theory consisting of large and uniform parts that look essentially like separate universes. The theory points to the existence of an endless sea of “mini universes” or “pocket universes” like our own where inflation has halted. The ramifications of this development are profound — it broadens the scope of all that is out there from universe to multiverse, an eternally flourishing fractal consisting of infinitely many self-similar pieces.
What’s more, Linde suggests that these pocket universes could give rise to different physical properties from the ones we experience in our universe. Linde’s multiverse mirrors that of an interstellar playhouse thriving with cartoonish novelty. Some pocket universes are springing with extraterrestrial life, while others grow unstable and collapse under their own weight. Some glow with entire systems of stars and galaxies bunched together, some have gamma rays spray radiant beams of energy into the singularities of quasars, others contain intelligent civilizations building an intergalactic Dyson sphere — and still others may be so alien and out-of-this-world from our plane of existence that we can barely even begin to understand their substance. There could be an infinite number of yourselves reading this article right now in replica universes, and an infinity more inhabiting near-replicas. There could be countless versions of you occupying parallel worlds in which events diverge in ways ranging from the could-have-been to the will-have-happened. In a fractal universe of ever-expanding universes, every possibility runs its course.
It certainly captures the imagination to wonder about the variety of universes that exists behind each astral rift — a fascination comparable to zooming into infinite fractals like the Mandelbrot set. While the insensate void past the edges of our universe may lie well beyond the reach of our corporeal bodies, that does not mean it is an inopportune time for humans to explore the multiverse. Luckily, fractal-generating software provides a suitable form to depict the myriad abstract spaces sprawling its bubble universes. Computer apps such as JWildfire, Mandelbulb 3D, Apophysis, and more can simulate the diverse worlds inhabited by fractals in picture form by amalgamating basic structures with resplendent colors and patterns. The products of this recent art form, fractal art, are equal parts bizarre and brilliant, like something straight out of a sci-fi art exhibition.
To this day, the theory of everything remains the unsolvable riddle it started off as. If its perfect statements of reality and nature are on the horizon, then perhaps we can anticipate a deluge of scientific breakthroughs in the coming decades, maybe centuries. And if it isn’t, well, science is constantly probing new questions to inch its way to the answers. Either way, we don’t really know where science is or where it is headed. There is still so much out there left to explore — just like zooming into a fractal, we might find ourselves nosing into the deepest rabbit-holes in pursuit of the dream. Whatever it is that reveals itself to be the key to unlocking the mysteries of the universe — whether it be the String Theory Landscape, quantum mechanics, the Riemann Hypothesis, or something else entirely — fractals tempt us down the bottomless phantasmagoria into the depths of infinity, and beyond!
Whatever it is that reveals itself to be the key to unlocking the mysteries of the universe — whether it be the String Theory Landscape, quantum mechanics, the Riemann Hypothesis, or something else entirely — fractals tempt us down the bottomless phantasmagoria into the depths of infinity, and beyond!
Rajin Tahsan is a Copy Chief for ‘The Science Survey.’ Rajin enjoys journalistic writing because it enables him to explore fascinating intersections...